COMPLEMENTACION

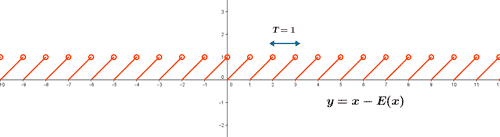
En la complementación de las inversas tenemos que algunas funciones explicadas anteriormente
en la temática tratada también se pueden identificar términos relacionados como lo son

Las Razones trigonométricas se definen comúnmente como el cociente entre dos lados de un triangulo rectángulo  asociado a sus ángulos.

 Las funciones trigonométricas son funciones cuyos valores son extensiones del concepto de razón trigonométrica en un triángulo rectángulo trazado en una circunferencia unitaria (de radio unidad). 

Definiciones más modernas las describen como series infinitas o como la solución de ciertas ecuaciones diferenciales, permitiendo su extensión a valores positivos y negativos, e incluso a números complejos.

Existen seis funciones trigonométricas básicas. Las últimas cuatro, se definen en relación de las dos primeras funciones, aunque se pueden definir geométricamente o por medio de sus relaciones. 

 Algunas funciones fueron comunes antiguamente, y aparecen en las primeras tablas, pero no se utilizan actualmente ; por ejemplo el ver seno  (1 − cos θ) y la ex secante (sec θ − 1).

Generalizando estas funciones pueden llegar a ser muy muy útiles. Pues hacen parte fundamental  en la carrera de arquitectos ó ingenieros que es en el campo en el que mas se usa esta proporción donde se trabaja o habla mas de ella.

continuación- FUNCIONES PERIÓDICAS

Como ya se ha explicado anteriormente las funciones trigonométricas inversas


 si los valores de la función se repiten conforme se añade a la variable independiente un determinado
de la misma manera, pero en un contexto físico las ondas periódicas que son aquellas ondas que muestran periodicidad  respecto del tiempo,es decir, describen ciclos repetitivos. En una onda periódica se cumple:

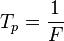donde el periodo propio fundamental ,  es la frecuencia de la componente fundamental de la onda periódica y  un número entero.

La forma más simple de onda periódica es la onda armónica. Esta onda está completamente caracterizada por tres parámetros: 1 la amplitud de la sinusoide , la frecuencia en radianes , por segundo y la fase en radianes. A menudo se usa la frecuencia F en ciclos por segundo

pero  el modelo descrito para las ondas armónicas no sirve para describir estructuras periódicas más complicadas: las ondas armónicas

Existen algunos valores característicos de las ondas periódicas 

El valor medio de una onda,es muy frecuente que el valor medio de una onda periódica sea cero. En electrotecnia y electrónica un valor medio no nulo mide la magnitud de un componente de

corriente continua ene una señal.

El valor eficaz, se calcula sobre un intervalo de la función correspondiente a un periodo propio fundamental completo el valor eficaz de una onda periódica es de especial interés en fisica cuando se aplica a presiones (mecánica), tensiones o intensidades (electrotecnia ó electrónica) para cálculos relacionados con la energía o la potencia. Con relación al valor máximo ..

A continuacion un ejemplo gráfico: 

Se explica una función periódica mas que todo como representación gráfica que se repite a intervalos regulares Esta propiedad las hace mas útiles para entender la multitud de fenómenos periódicos que se dan en nuestro mundo Su estudio matemático se hace posilbe gracias al uso de las funciones seno y coseno.

 

FUNCIONES PERIÓDICAS.

Las funciones periódicas son aquellas que se repiten cada intervalo

y = f(x) donde f(x) es periódica.

Se llama función inversa o recíproca de f a otra función f^-1 que cumple que:

Si f(a) = b, entonces f⁻¹(b) = a.

Por otra parte si se quiere hallar el recorrido de una función tenemos que hallar el dominio de su función inversa.

si dos funciones son inversas su composición es la función identidad

Las gráficas de F y F-1 son simétricas con respecto a la bisectriz del primer y tercer cuadrante.

características de algunas de las funciones:  

función seno:  el dominio dela función seno son los números reales 

las imágenes son los resultados para cada x hay un resultado que este entre 0 y 1

la función seno en el primer cuadrante crece de cero a tt/2 en el segundo cuadrante decrece de tt/2 a tt en el tercer decrece de tt a 3tt/2 a 2tt

la linea es periódica cada 2tt. 

función coseno: el dominio son todos los números reales

es continua 

es una función periódica donde el periodo es 2tt

el valor mínimo de coseno es -1 y el máximo es 1

el coseno decrece de cero hasta 2tt

el coseno crece desde tt a 2tt.

 función cotangente:

en cero no esta definida 

es periódica su periodo es 2tt.

continuación- INVERSAS TRIGONOMETRICAS

Las demás funciones trigonométricas se relacionan de igual manera para estas

• la cosecante tambien abreviado como csc  o cosec es la razón inversa de seno, o también su inverso multiplicativo:

csc alfa = 1/sen alfa=  c/a

Para la  Tangente y cotangente se presenta..

TANGENTE INVERSA..

 

COTENGENTE  INVERSA..

FUNCIONES INVERSAS

Las tres funciones trigonométricas inversas usadas de manera comun son:

 arcoseno es la función inversa del seno del ángulo.

 arcocoseno: es la función inversa del coseno del ángulo.

 arcotangente: es la función inversa de la tangente del ángulo.

 una función es la relación entre dos conjuntos que obedecen a leyes como que un elemento del conjunto de partida puede estar relacionado con uno y uno solo elemento del conjunto arribo, pero que elemnto de arribo puede estar relacionado con mas de un elemento del conjunto de partida..

pues bien la función inversa es caviar el conjunto de partida por el de arribo y el de llegada por el de parten za,,,

la única propiedad que se debe  tener  en cuenta, es que sea  invertible si y solo si es biyectiva, biyectiva significa si un elemento del conjunto partenza le corresponde uno solo de elemento llegada y viceversa, a un elemento del conjunto arribo le corresponde uno solo del conjunto partida y que no quede elementos libres sin estar relacionados.   

 por ejemplo:

 f(x)=y
la inversa: x=f(y)

A continuación un ejemplo gráficamente

FUNCIÓN SENO

SU INVERSA ES:

Algunas de las características que presentan estas inversas son:
Los dominios de algunas de estas funciones son todos los números reales
tienen al igual que las funciones algunas propiedades.

el teorema de la función inversa  proporciona las condiciones suficientes para que una aplicación sea invertible local mente en un entorno de un punto p en términos de su derivada eneste punto. Técnicamente es un teorema de existencia local de la función inversa,,

las funciones trigonometricas inversas son relaciones pero  si se restringe el dominio la función trigonométrica se establece una relación biunívoca y la inversa de la función trigonométrica pasa a se r una función.